BFS

算法：

#define     MAXSIZE    100
bool visited[MAXSIZE]; //访问数组，用来记录各个顶点是否被访问过；
//v： 调用本函数，用来访问第v个顶点的下标；
void BFS(Graph G, int v)
{
    //定义一个指向边表的临时指针: 
    ArcNode *p;
    //初始化队列:
    InitQueue(Q);
    //访问: 伪代码 E.g printf
    visit(v);
    //表示下标为v对应的顶点被访问过了: 
    visited[v] = TRUE;
    //入队: 目的是在下面的循环中遍历该v对应的结点对应的所有结点
    EnQueue(Q,v);
    //如果队列不为空:
    //该队列存在的意义：将队列中每个顶点对应的下个顶点的所有结点访问完毕
    while(!isEmpty(Q))
    {
        //出队: 将队列中存放的结点所在的数组中的下标给临时变量v.
        DeQueue(Q,v);
        //获取图G中数组adjList下标为v值的顶点的第1条边，把该边的地址赋值给临时变量p:
        p = G->adjList[v].firstedge;
        //如果该p指向的顶点的地址存在：
        while(p)
        {
            //如果该p指向的顶点对应的visited数组对应的标记不是0(即没有被访问)的话:
            if(!visited[p->adjvex])
            {
                //访问:
                visit(p->adjvex);
                //标记该顶点访问过了:
                visted[p->adjvex] = TRUE;
                //将该顶点入栈: 实际上最坏的情况，将连通图中每个有关系的结点都入队了 ^_^
                EnQueue(Q,p->adjvex);
            }
            //让p指向当前顶点的下个顶点:
            p = p->next;
        }
    }
}

举例：

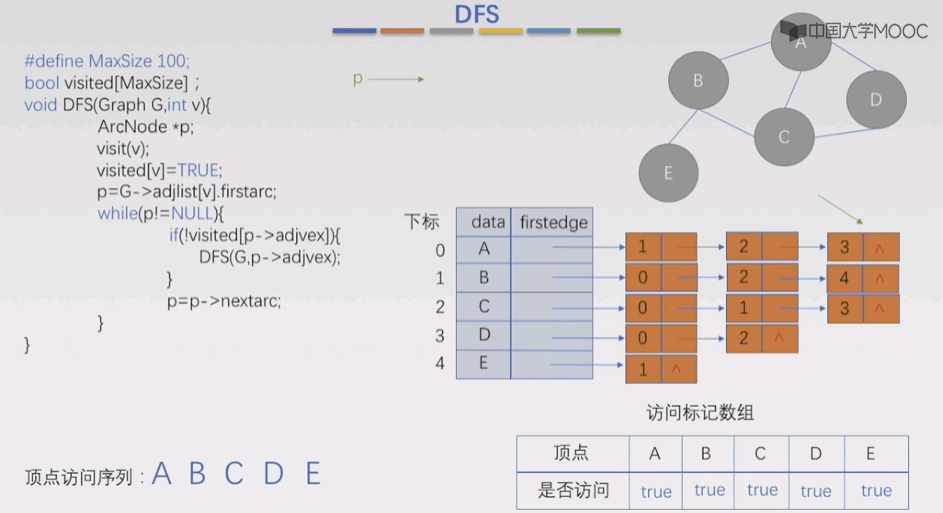
DFS

#define     MAXSIZE    100
bool visited[MAXSIZE]; //访问数组，用来记录各个顶点是否被访问过；
//v： 调用本函数，用来访问第v个顶点的下标；
void DFS(Graph G, int v)
{
    //定义一个指向边表的临时指针: 
    ArcNode *p;
    //初始化队列:
    InitQueue(Q);
    //访问: 伪代码 E.g printf
    visit(v);
    //表示下标为v对应的顶点被访问过了: 
    visited[v] = TRUE;
    p=G->adjlist[v].firstarc;   //指针p开始指向该顶点的第一条边
    //如果p指向的结点地址存在的话：
    while(p!=NULL)
    {         
        //没遍历完顶点的所有邻接顶点：
        if(!visited[p->adjvex])
        {   
            //如果该顶点没被访问，那么就递归访问该顶点
            DFS(G,p->adjvex); 
        }
        p=p->nextarc;   //看还有没有其他未访问的顶点
    }
}

void DFSTraverse(Graph  G)
{
    int i;  //单独定义是为了方便多个循环中使用
    for(i=0; i<G->vexnum; i++）
    {
        visited[i]=false; //将标志数组初始化 (全局数组)
    }
    for(i=0; i<G->vexnum; i++)
    {
        if(!visited[i])
        {
            DFS(G,i);   //对所有
        }
    }
}